روش های زیادی برای حل معادلات غیر خطی در متلب وجود دارد که در زیر به شرح آنها می پردازیم:
1-روش هایی که همگرایی آنها تضمین شده است(محدوده معین)
1-1-Bisection یا روش نصف کردن محدوده
2-1-False Position یا روش درون يابی خطی
2-روش هایی که تضمین همگرایی ندارند(روش باز-معمولا سریع تر هستند)
1-2-Fixed-Point Iteration روش تکرار
2-2-Secant Methods روش وتری
3-2-Newton-Raphson روش نيوتن رافسون
در این مطلب روش نصف کردن محدوده یا همان Bisection را تشریح می کنیم و انشالله در مطالب آینده روش های دیگر به ترتیب بیان خواهند شد.
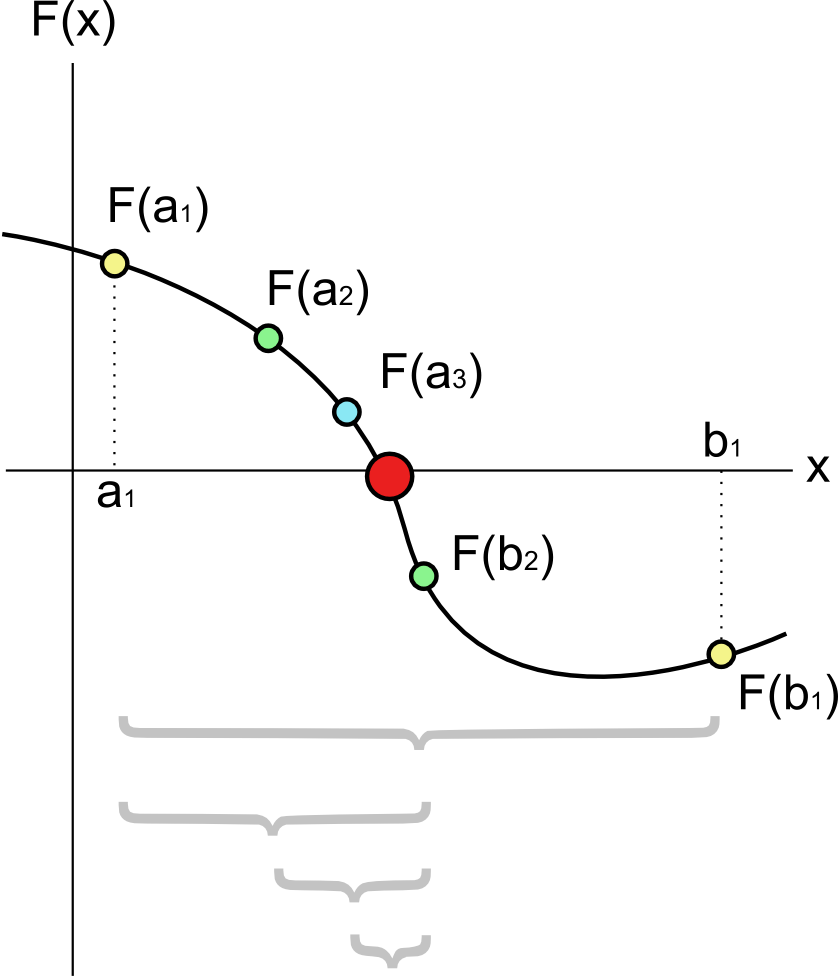
روش نصف کردن (Bisection Method):
در این روش برای بدست آوردن ریشه معادله بازه ی معینی موجود می باشد و الگوریتم به شکل زیر می باشد:
1)ابتدا بازه ای که مطمئن هستیم ریشه در آن است را تعیین می کنیم.مثلا [a b] که برای تعیین اینکه ریشه در این بازه است باید:
f(a)*f(b)<0
2)در صورت درستی رابطه بالا مطمئن هستیم حداقل یک ریشه در بازه وجود دارد.
x=(a+b)/2
3)حال درستی رابطه زیر را بررسی می کنیم:
f(a)*f(x)<0
4)اگر درست بود یعنی ریشه بین a و x می باشد و مقدار x در b قرار می گیرد و به مرحله 2 برمیگردیم، در غیر این صورت مقدار x در a قرار می گیرد و به مرحله 2 باز میگردیم و تکرار را تا زمان رسیدن به دقت خواسته شده ادامه می دهیم.
function روش bisection:
function [r er his] = bis(f,a,b,tel,maxit)
% f=function is defined in M-file
% r=root
% a/b = initial left/right point of the solution interval
% tel=upperbound of error
% his=history of r
% er=(b - a)/2(half the last interval width),error
% maxint= maximum of iterations
fa=feval(f,a);fb=feval(f,b);
if(fa*fb>0)
error('We must have f(a)f(b)<0!')
end
for k=1:maxit
his(k)=(a+b)/2;
fr=feval(f,his(k));
er=(b-a)/2;
if(abs(fr)<eps || abs(er)<tel);break;
elseif(fr*fa>0) fa=fr;a=his(k);
else b=his(k);
end
end
r=his(k);
end
function تابع غیر خطی:
function y = f(x) y=x.^2-1; end
کد تایپ شده در پنجره دستور برای محاسبه ریشه تابع f
[root error history]=bis('f',-2,-0.5,0.001,1000)
نتیجه run :
root = -1.0002 error = 7.3242e-04 history = Columns 1 through 6 -1.2500 -0.8750 -1.0625 -0.9688 -1.0156 -0.9922 Columns 7 through 11 -1.0039 -0.9980 -1.0010 -0.9995 -1.0002