فراریت نسبی (Relative volatility)
فراریت نسبی عبارت است از نسبت غلظت های A و B در یک فاز به همین نسبت در فاز دوم
\(α_{AB}={{({y_A \over y_B})_\text{بخار}} \over {({x_A \over x_B})_\text{مایع}}}={y_A \over x_A} ×{x_B \over y_B}\)
مقدار \(α\) با x تغییر می کند. اگر \(x_A=y_A\) باشد (به استثنای \(x=0,1 \)) مقدار \(α\) برابر واحد بوده و جداسازی امکانپذیر نخواهد بود. هر چه مقدار \(α\) بزرگتر از واحد باشد، جداسازی راحت تر صورت می گیرد.
ضریب توزیع یک سازنده در دو فاز
ضریب توزیع به صورت زیر تعریف می شود:
\(k_A= {y_A \over x_A} \)
رابطه ضریب فراریت نسبی و ضریب توزیع به صورت زیر بیان می شود.
\( α_{AB}= {k_A \over k_B} \)
نکته: ضریب توزیع تابعی از دما، فشار و نوع ماده است. با افزایش دما و یا کاهش فشار، k زیاد می شود.
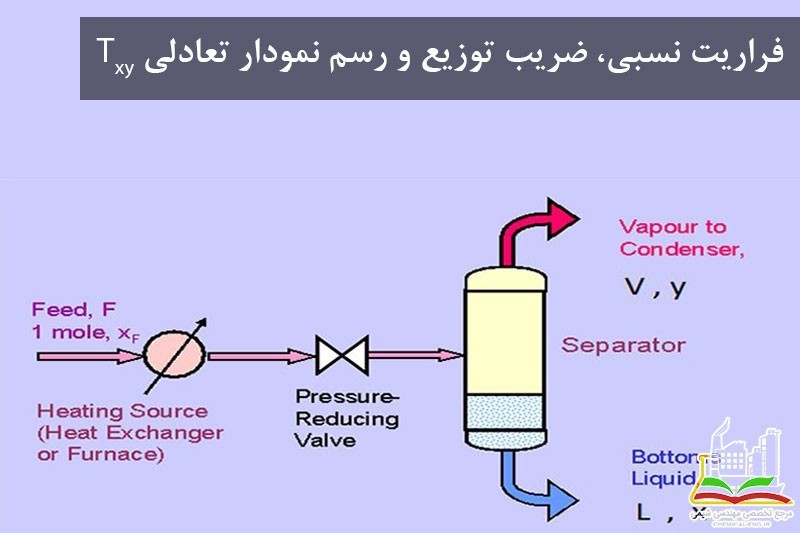
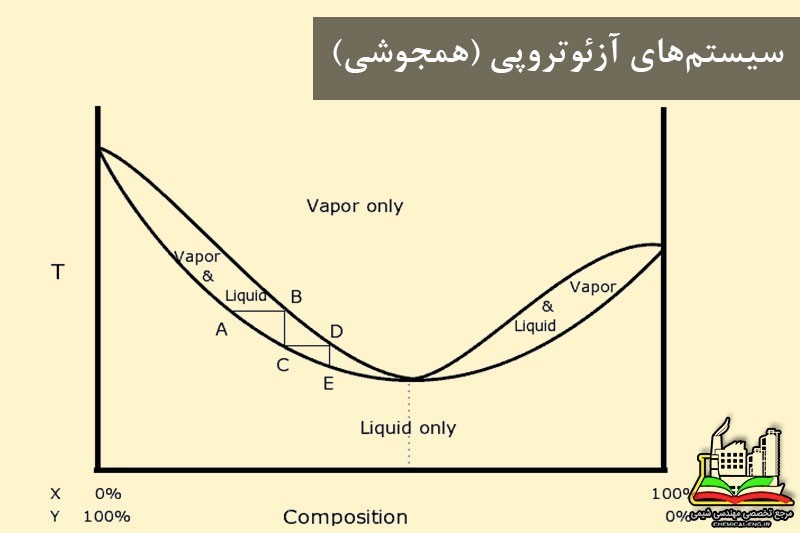
رسم منحنی \(T_{xy}\) و xy
برای رسم این نوع منحنی ها معمولا از سه روش استفاده می شود:
- با استفاده از داده های تجربی
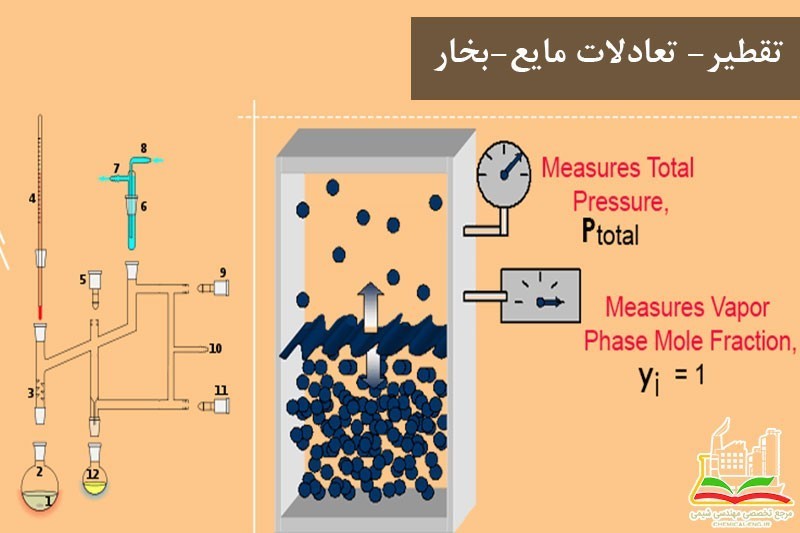
کمیات تعادلی فاز بخار و مایع را به استثنای حالاتی که با محلول های کامل و یا بسامان سروکار داریم، باید به روش های تجربی تعیین کرد.
- با استفاده از قوانین رائولت و دالتون
در محلولهای کامل، فشار جزئی تعادلی هر سازنده در دمای ثابت، برابر با حاصلضرب فشار بخار سازنده خالص در آن دما در جزء مولی آن سازنده در مایع است.
برای محلول های ایدال قانون رائولت به صورت زیر بیان می شود:
\( P_A= x_A {P_A}^{sat}\)
\( P_B= x_B {P_B}^{sat}= (1-x_A) {P_B}^{sat} \)
نکته: شرط اصلی که یک محلول ایدال باشد، این است که اجزاء از نظر شیمیایی شبیه به هم باشند.
اگر فاز بخار نیز کامل باشد، داریم:
\( P_t= P_A +P_B= x_A {P_A}^{sat} +(1-x_A) {P_B}^{sat} ={P_B}^{sat} +x_A ({P_A}^{sat} –{P_B}^{sat})\)
نکته:
برای اینکه بتوان بخار را کامل گرفت باید فشار آن پایین یا متوسط باشد.
در این حالت فشار کل و فشارهای جزئی در دمای ثابت، توابعی خطی از x هستند.
با استفاده از روابط فوق داریم:
\( x_A={{P_t-{P_B}^{sat}} \over {{P_A}^{sat}-{P_B}^{sat}}}\)
\( y_A= {{P_A} \over {P_B}}={{{{P_A}^{sat}} \over {P_t}} x_A}\)
با استفاده از تعریف ضریب توزیع داریم:
\( k_A= {{y_A} \over {x_A}}={{{P_A}^{sat}} \over {P_t}} \)
\( k_B= {{y_B} \over {x_B}}={{{P_B}^{sat}} \over {P_t}} \)
برای ماده خالص از رابطه آنتوان می توان فشار بخار را در هر دمایی محاسبه کرد.
\( log {P^{sat}}=A-{B \over {T+C}}\)
که A، B، C ثابت های آنتوان، T دما بر حسب کلوین و P فشار بر حسب mmHg می باشد.
- با استفاده از ضریب فراریت نسبی ثابت
\( α_{AB}= {{y_A \over x_A} ×{x_B \over y_B}}={{y_A/(1-y_A)} \over {x_A (1-x_A)} }\)
\( y_A={{ α_{AB} x_A} \over {1+( α_{AB}-1)x_A}}\)
نکته: اگر α تغییر کند و بخواهیم از این روش استفاده کنیم برای تغییرات کم و زیاد α به ترتیب از میانگین حسابی و هندسی استفاده می کنیم.
در محلول های کامل داریم:
\( α_{AB}= {P_A \over P_B }={{ {P_A}^{sat}} \over { {P_B}^{sat}}} \approx cte\)